Unsupervised Learning: Neighbor Embedding

本文介绍了非线性降维的一些算法，包括局部线性嵌入LLE、拉普拉斯特征映射和t分布随机邻居嵌入t-SNE，其中t-SNE特别适用于可视化的应用场景

PCA和Word Embedding介绍了线性降维的思想，而Neighbor Embedding要介绍的是非线性的降维

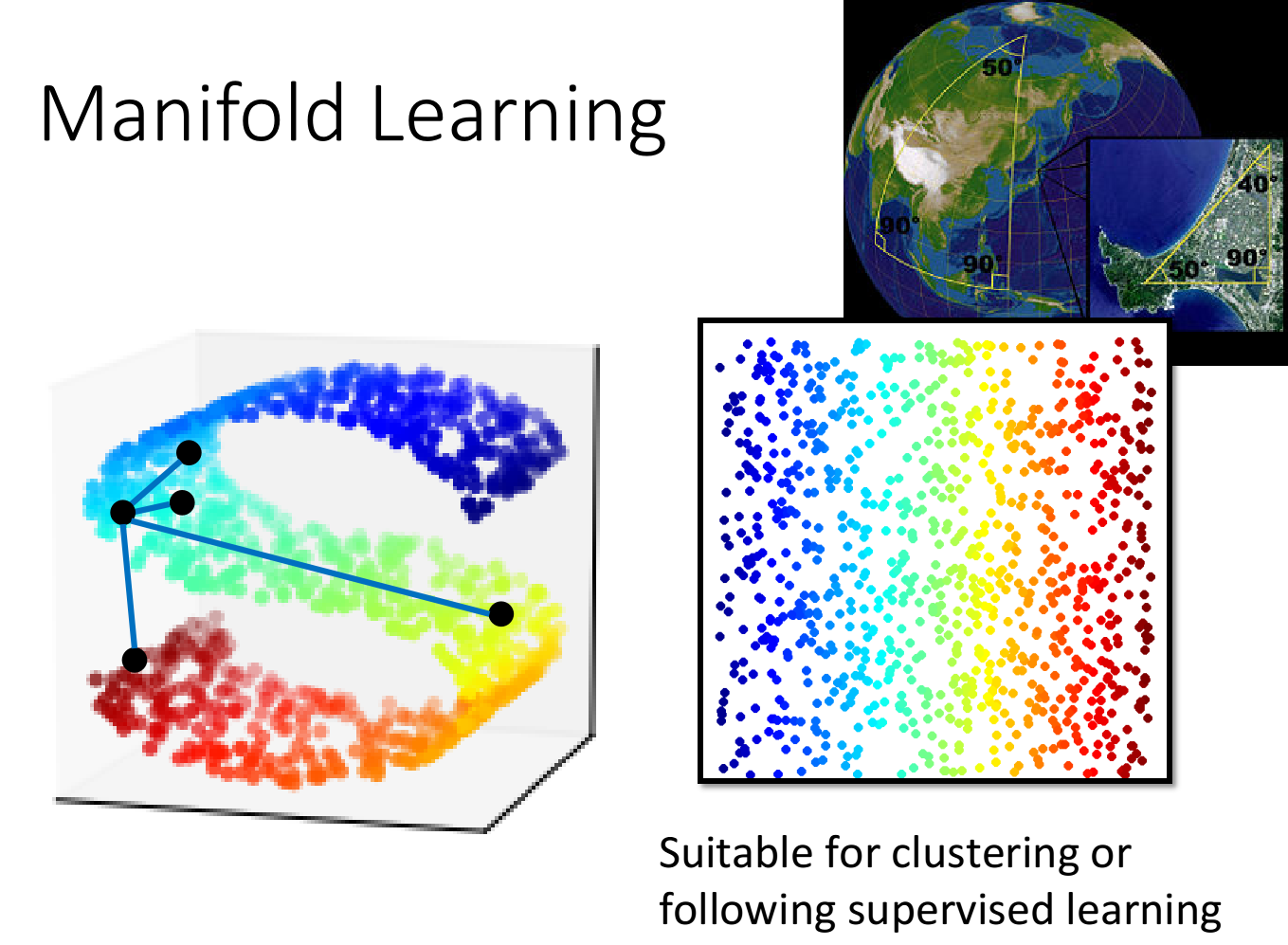
Manifold Learning

样本点的分布可能是在高维空间里的一个流行(Manifold)，也就是说，样本点其实是分布在低维空间里面，只是被扭曲地塞到了一个高维空间里

地球的表面就是一个流行(Manifold)，它是一个二维的平面，但是被塞到了一个三维空间里

在Manifold中，只有距离很近的点欧氏距离(Euclidean Distance)才会成立，而在下图的S型曲面中，欧氏距离是无法判断两个样本点的相似程度的

而Manifold Learning要做的就是把这个S型曲面降维展开，把塞在高维空间里的低维空间摊平，此时使用欧氏距离就可以描述样本点之间的相似程度

Locally Linear Embedding

局部线性嵌入，locally linear embedding，简称LLE

假设在原来的空间中，样本点的分布如下所示，我们关注$x^i$和它的邻居$x^j$，用$w_{ij}$来描述$x_i$和$x_j$的关系

假设每一个样本点$x^i$都是可以用它的neighbor做linear combination组合而成，那$w_{ij}$就是拿$x^j$去组合$x^i$时的权重weight，因此找点与点的关系$w_{ij}$这个问题就转换成，找一组使得所有样本点与周围点线性组合的差距能够最小的参数$w_{ij}$：

$$\sum _i||x^i-\sum _j{w}_{ij}{x}^j|{|}_2$$

接下来就要做Dimension Reduction，把$x^i$和$x^j$降维到$z^i$和$z^j$，并且保持降维前后两个点之间的关系$w_{ij}$是不变的

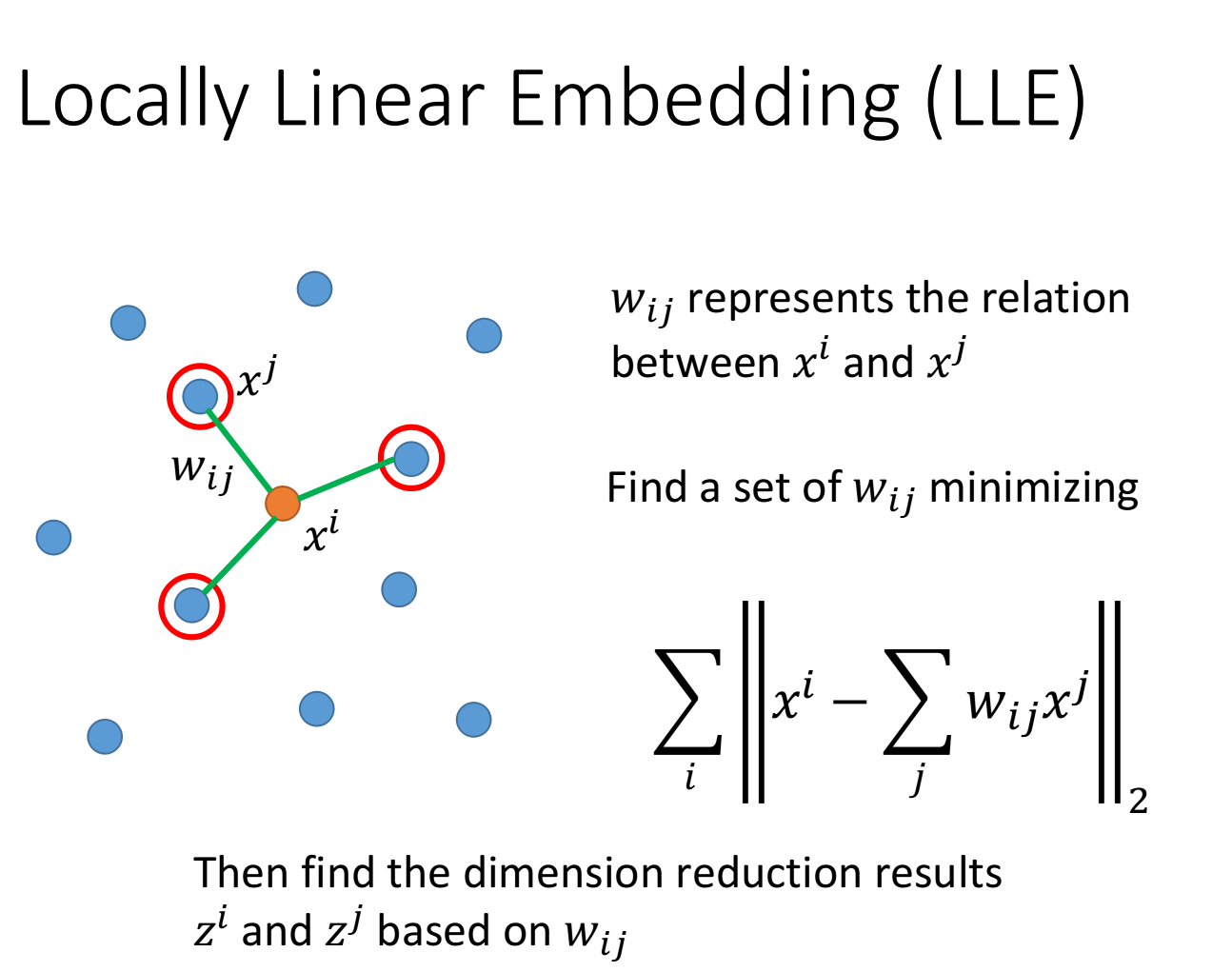
LLE的具体做法如下：

• 在原先的高维空间中找到$x^i$和$x^j$之间的关系$w_{ij}$以后就把它固定住

• 使$x^i$和$x^j$降维到新的低维空间上的$z^i$和$z^j$

• $z^i$和$z^j$需要minimize下面的式子：

  $$\sum _i||z^i-\sum _j{w}_{ij}{z}^j|{|}_2$$

• 即在原本的空间里，$x^i$可以由周围点通过参数$w_{ij}$进行线性组合得到，则要求在降维后的空间里，$z^i$也可以用同样的线性组合得到

实际上，LLE并没有给出明确的降维函数，它没有明确地告诉我们怎么从$x^i$降维到$z^i$，只是给出了降维前后的约束条件

在实际应用LLE的时候，对$x^i$来说，需要选择合适的邻居点数目K才会得到好的结果

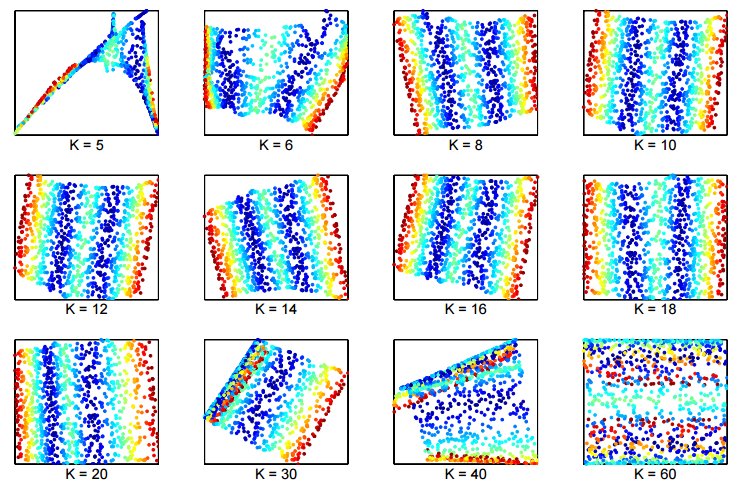
下图给出了原始paper中的实验结果，K太小或太大得到的结果都不太好，注意到在原先的空间里，只有距离很近的点之间的关系需要被保持住，如果K选的很大，就会选中一些由于空间扭曲才导致距离接近的点，而这些点的关系我们并不希望在降维后还能被保留

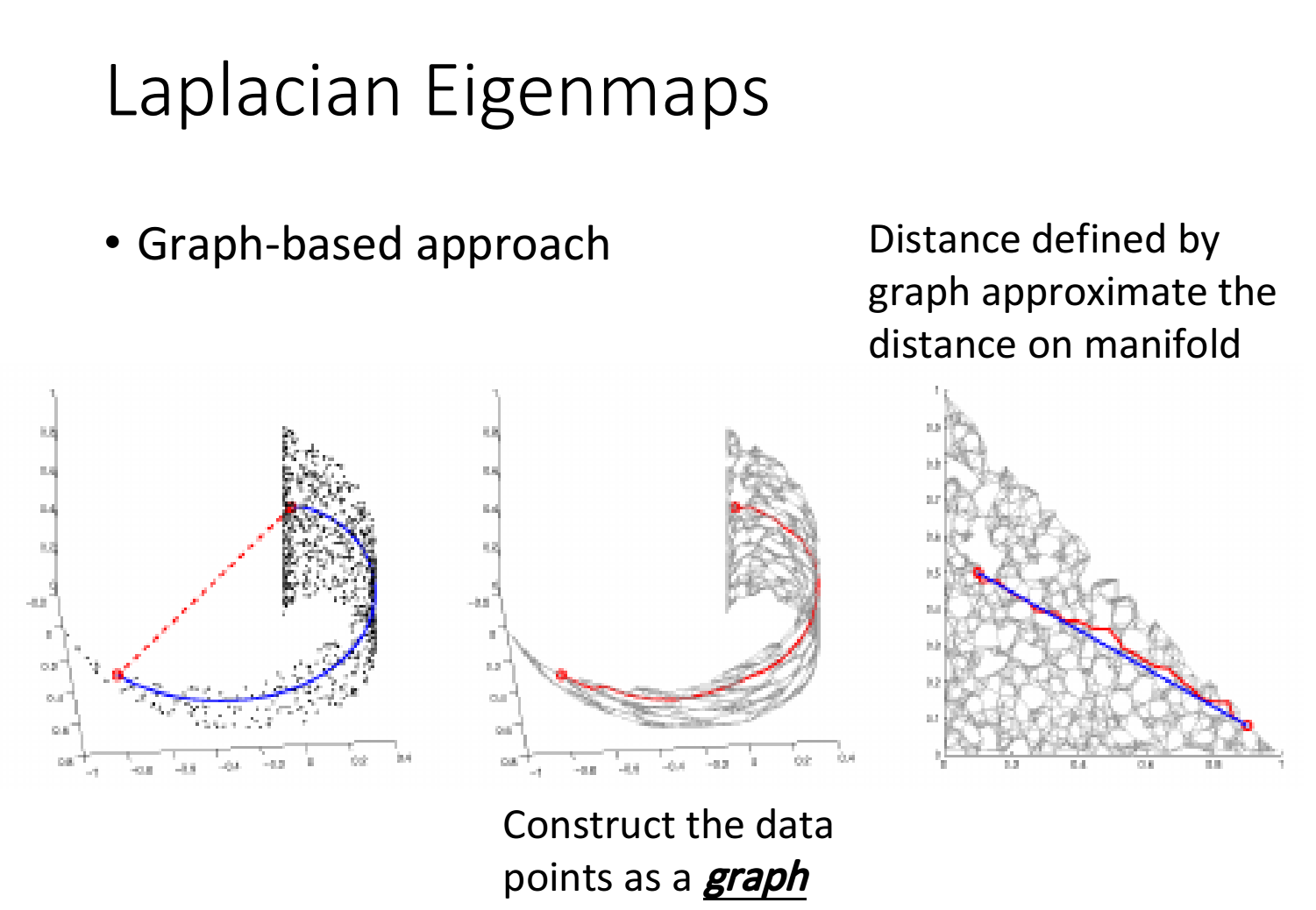
Laplacian Eigenmaps

Introduction

另一种方法叫拉普拉斯特征映射，Laplacian Eigenmaps

之前在semi-supervised learning有提到smoothness assumption，即我们仅知道两点之间的欧氏距离是不够的，还需要观察两个点在high density区域下的距离

如果两个点在high density的区域里比较近，那才算是真正的接近

我们依据某些规则把样本点建立graph，那么smoothness的距离就可以使用graph中连接两个点路径上的edges数来近似

Review for Smoothness Assumption

简单回顾一下在semi-supervised里的说法：如果两个点$x^1$和$x^2$在高密度区域上是相近的，那它们的label $y^1$和$y^2$很有可能是一样的

$$\begin{gathered} L=\sum _{x^r}C(y^r,{\hat{y}}^r)+\lambda S \\ S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i-y^j{)}^2=y^{T}Ly \end{gathered}$$

其中$C(y^r,{\hat{y}}^r)$表示labeled data项，$\lambda S$表示unlabeled data项，它就像是一个regularization term，用于判断我们当前得到的label是否是smooth的

其中如果点$x^i$与$x^j$是相连的，则$w_{i,j}$等于相似度，否则为0，$S$的表达式希望在$x^i$与$x^j$很接近的情况下，相似度$w_{i,j}$很大，而label差距$|y^i-y^j|$越小越好，同时也是对label平滑度的一个衡量

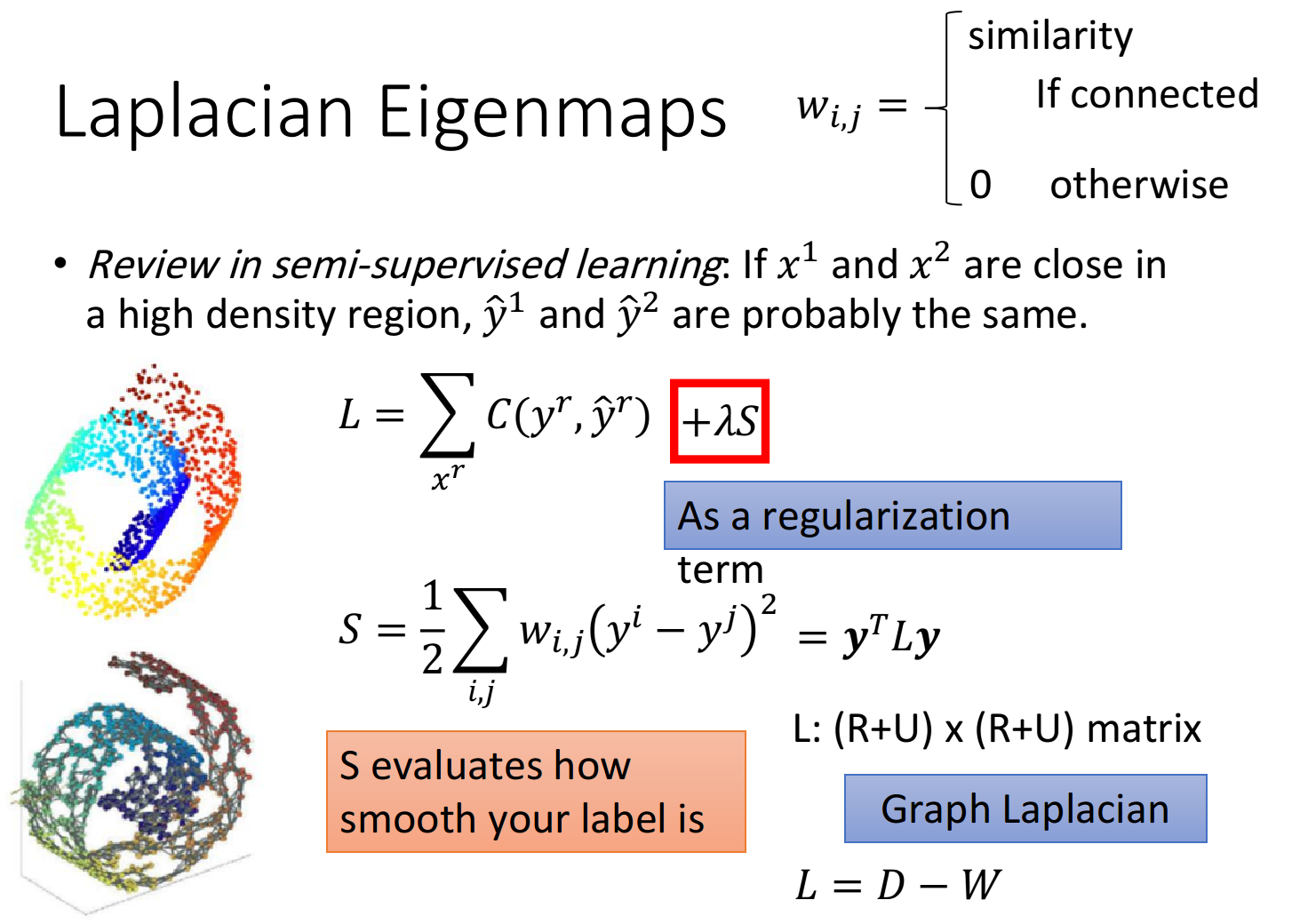
Application in Unsupervised Task

降维的基本原则：如果$x^i$和$x^j$在high density区域上是相近的，即相似度$w_{i,j}$很大，则降维后的$z^i$和$z^j$也需要很接近，总体来说就是让下面的式子尽可能小

$$S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i-y^j{)}^2$$

注意，与LLE不同的是，这里的$w_{i,j}$表示$x^i$与$x^j$这两点的相似度，上式也可以写成$S=\sum _{i,j}{w}_{i,j}||z^i-z^j|{|}_2$

但光有上面这个式子是不够的，假如令所有的z相等，比如令$z^i=z^j=0$，那上式就会直接停止更新

在semi-supervised中，如果所有label $z^i$都设成一样，会使得supervised部分的$\sum _{x^r}C(y^r,{\hat{y}}^r)$变得很大，因此lost就会很大，但在这里少了supervised的约束，因此我们需要给$z$一些额外的约束：

• 假设降维后$z$所处的空间为$M$维，则$\{z^1,z^2,...,z^N\}=R^M$，我们希望降维后的$z$占据整个$M$维的空间，而不希望它活在一个比$M$更低维的空间里
• 最终解出来的$z$其实就是Graph Laplacian $L$比较小的特征值所对应的特征向量

这也是Laplacian Eigenmaps名称的由来，我们找的$z$就是Laplacian matrix的特征向量

如果通过拉普拉斯特征映射找到$z$之后再对其利用K-means做聚类，就叫做谱聚类(spectral clustering)

注：有关拉普拉斯图矩阵的相关内容可参考之前的半监督学习笔记：15_Semi-supervised Learning

参考文献：Belkin, M., Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Advances in neural information processing systems . 2002

t-SNE

t-SNE，全称为T-distributed Stochastic Neighbor Embedding，t分布随机邻居嵌入

Shortage in LLE

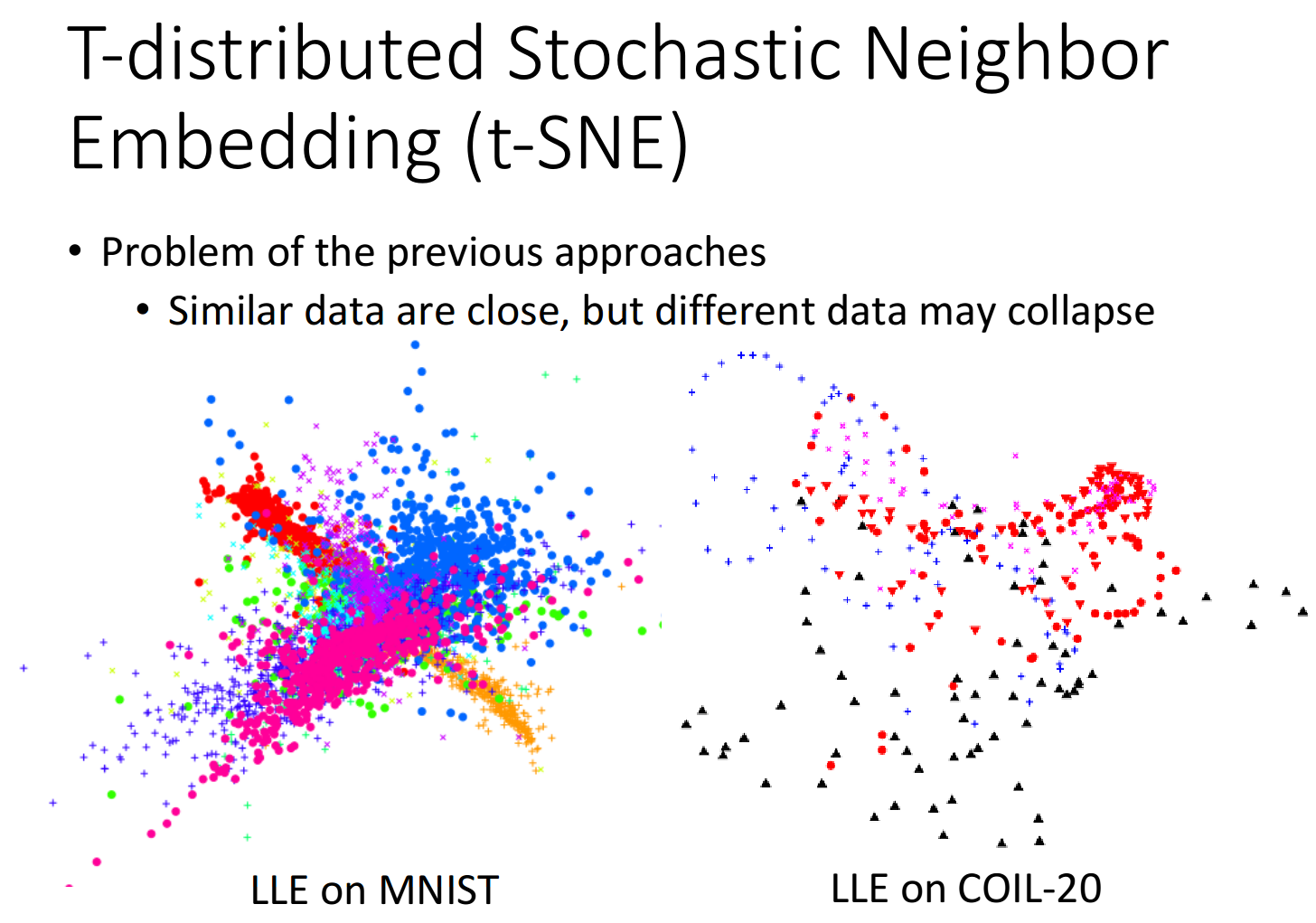
前面的方法只假设了相邻的点要接近，却没有假设不相近的点要分开

所以在MNIST使用LLE会遇到下图的情形，它确实会把同一个class的点都聚集在一起，却没有办法避免不同class的点重叠在一个区域，这就会导致依旧无法区分不同class的现象

COIL-20数据集包含了同一张图片进行旋转之后的不同形态，对其使用LLE降维后得到的结果是，同一个圆圈代表同张图像旋转的不同姿态，但许多圆圈之间存在重叠

How t-SNE works

做t-SNE同样要降维，在原来$x$的分布空间上，我们需要计算所有$x^i$与$x^j$之间的相似度$S(x^i,x^j)$

然后需要将其做归一化：$P(x^j|x^i)=\frac{S(x^i,x^j)}{\sum _{k\ne i}S(x^i,x^k)}$，即$x^j$与$x^i$的相似度占所有与$x^i$相关的相似度的比例

将$x$降维到$z$，同样可以计算相似度$S^{\prime }(z^i,z^j)$，并做归一化：$Q(z^j|z^i)=\frac{S^{\prime }(z^i,z^j)}{\sum _{k\ne i}{S}^{\prime }(z^i,z^k)}$

注意，这里的归一化是有必要的，因为我们无法判断在$x$和$z$所在的空间里，$S(x^i,x^j)$与$S^{\prime }(z^i,z^j)$的范围是否是一致的，需要将其映射到一个统一的概率区间

我们希望找到的投影空间$z$，可以让$P(x^j|x^i)$和$Q(z^j|z^i)$的分布越接近越好

用于衡量两个分布之间相似度的方法就是KL散度(KL divergence)，我们的目标就是让$L$越小越好：

$$\begin{gathered} L=\sum _{i}KL(P(\ast |x^i)||Q(\ast |z^i)) \\ =\sum _i\sum _{j}P(x^j|x^i)log\frac{P(x^j|x^i)}{Q(z^j|z^i)} \end{gathered}$$

KL Divergence

这里简单补充一下KL散度的基本知识

KL 散度，最早是从信息论里演化而来的，所以在介绍 KL 散度之前，我们要先介绍一下信息熵，信息熵的定义如下：

$$H=-\sum _{i=1}^{N}p(x_i)\cdot logp(x_i)$$

其中$p(x_i)$表示事件$x_i$发生的概率，信息熵其实反映的就是要表示一个概率分布所需要的平均信息量

在信息熵的基础上，我们定义KL散度为：

$$\begin{gathered} D_{KL}(p||q)=\sum _{i=1}^{N}p(x_i)\cdot (logp(x_i)-logq(x_i)) \\ =\sum _{i=1}^{N}p(x_i)\cdot log\frac{p(x_i)}{q(x_i)} \end{gathered}$$

$D_{KL}(p||q)$表示的就是概率$q$与概率$p$之间的差异，很显然，KL散度越小，说明概率$q$与概率$p$之间越接近，那么预测的概率分布与真实的概率分布也就越接近

How to use

t-SNE会计算所有样本点之间的相似度，运算量会比较大，当数据量大的时候跑起来效率会比较低

常见的做法是对原先的空间用类似PCA的方法先做一次降维，然后用t-SNE对这个简单降维空间再做一次更深层次的降维，以期减少运算量

值得注意的是，t-SNE的式子无法对新的样本点进行处理，一旦出现新的$x^i$，就需要重新跑一遍该算法，所以t-SNE通常不是用来训练模型的，它更适合用于做基于固定数据的可视化

t-SNE常用于将固定的高维数据可视化到二维平面上

Similarity Measure

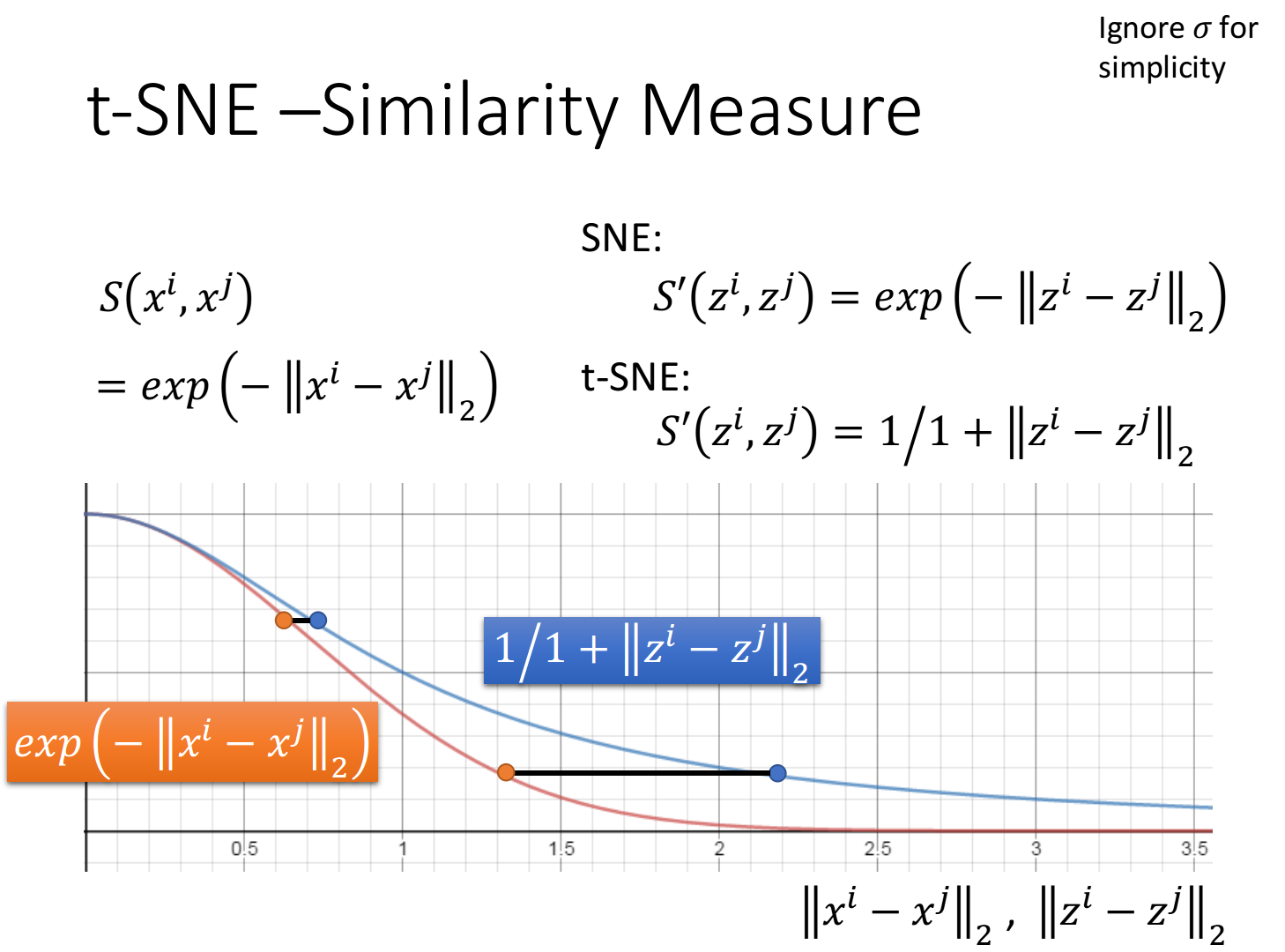
如果根据欧氏距离计算降维前的相似度，往往采用RBF function $S(x^i,x^j)=e^{-||x^i-x^j|{|}_2}$，这个表达式的好处是，只要两个样本点的欧氏距离稍微大一些，相似度就会下降得很快

还有一种叫做SNE的方法，它在降维后的新空间采用与上述相同的相似度算法$S^{\prime }(z^i,z^j)=e^{-||z^i-z^j|{|}_2}$

对t-SNE来说，它在降维后的新空间所采取的相似度算法是与之前不同的，它选取了t-distribution中的一种，即$S^{\prime }(z^i,z^j)=\frac{1}{1+||z^i-z^j|{|}_2}$

以下图为例，假设横轴代表了在原先$x$空间上的欧氏距离或者做降维之后在$z$空间上的欧氏距离，红线代表RBF function，是降维前的分布；蓝线代表了t-distribution，是降维后的分布

你会发现，降维前后相似度从RBF function到t-distribution：

• 如果原先两个点距离($\mathrm{\Delta }x$)比较近，则降维转换之后，它们的相似度($\mathrm{\Delta }y$)依旧是比较接近的
• 如果原先两个点距离($\mathrm{\Delta }x$)比较远，则降维转换之后，它们的相似度($\mathrm{\Delta }y$)会被拉得更远

也就是说t-SNE可以聚集相似的样本点，同时还会放大不同类别之间的距离，从而使得不同类别之间的分界线非常明显，特别适用于可视化，下图则是对MNIST和COIL-20先做PCA降维，再做t-SNE降维可视化的结果：

Conclusion

小结一下，本文主要介绍了三种非线性降维的算法：

• LLE(Locally Linear Embedding)，局部线性嵌入算法，主要思想是降维前后，每个点与周围邻居的线性组合关系不变，$x^i=\sum _j{w}_{ij}{x}^j$、$z^i=\sum _j{w}_{ij}{z}^j$
• Laplacian Eigenmaps，拉普拉斯特征映射，主要思想是在high density的区域，如果$x^i$、$x^j$这两个点相似度$w_{i,j}$高，则投影后的距离$||z^i-z^j|{|}_2$要小
• t-SNE(t-distribution Stochastic Neighbor Embedding)，t分布随机邻居嵌入，主要思想是，通过降维前后计算相似度由RBF function转换为t-distribution，在聚集相似点的同时，拉开不相似点的距离，比较适合用在数据固定的可视化领域